By sound we normally mean the sensation produced in our ears. Physically sound is produced by the vibration of objects like the vocal chords, stretched string of the Veena, the air column of the flute, the reed in the harmonium or simply the quick vibration of any object when it is struck. The vibrations have to reach the ear through a medium, usually the air. The air molecules surrounding the object producing the sound vibrate and the vibrations spread out in the form of 'waves' (by which we mean a disturbance moving through a medium while the medium itself undergoes only a to and fro movement at every point). When the wave reaches the ear, the ear drum vibrates in a manner similar to the original object and the vibrations are conveyed to the inner ear where fine hair follicle like objects vibrate and convey the sensation to the brain through nerves. When objects vibrate at frequencies higher than or lower than what we can hear they are referred to as ultrasonic and subsonic sound. Some animals (dogs especially) are sensitive to high frequency sounds.
Three essential qualities of any sound- in particular musical sound are pitch, loudness and quality. These are the sensations produced in the person hearing the sound. They have their physical equivalents in frequency, intensity and harmonic content which are quantities that can be measured.
Frequency is the number of times the original object (string or air column) or the eardrum vibrates (makes a complete to and fro motion) every second. The higher the frequency the higher is the pitch. In music the pitch is usually referred to by the note name like sa, ri, C,D etc. but when discussing as a physical entity the frequency number is taken as referring to the pitch. Pitch is actually the sensation felt by the listener. Extraneous factors can make the pitch of two sounds of the same frequency appear different. Human ears are sensitive to the frequency range from 30 cycles per sec to 15000 cycles per second - the sensitivity to higher frequency falling at old age which explains the difficulty in distinguishing words although the sound is heard as vowels and consonants are identified by frequencies of the higher harmonics. Most of the sounds we hear are usually well below 3000 cycles but the presence of higher frequency harmonics affects the quality and clarity in speech (see later). To appreciate how sounds of different frequencies feel, you can set the frequency below and hear it. (Youngsters may be able to hear 12000 cycles but as one grows older sensitivity to higher frequencies becomes less. Over 80 one may not be able to hear above 5000!)
Use the slider to choose frequency or enter (between 50 and 15000)
and click
100 15000
100 15000
Loudness is a term well understood. Its physical equivalent is the intensity of the sound which can be measured by the energy it contains or more simply by the amplitude of the vibration (ex. the extent to which the Veena string is displaced from its normal position). When sound is recorded digitally into a .wav or similar file the extent to which the numbers deviate from the zero (no sound) position decides the loudness. Below are the graphs drawn from part of a digital data of a violin sound at 2 levels of loudness. You can click on them to hear the sounds. (The graphs shown cover only about 1.3% of the duration of the total sound you hear.)
Quality is a term more difficult to define. We speak of dull tone, rich tone, good voice or the good timbre of a musical instrument. We also recognize consonants and vowels though spoken in different pitches.
When the string of a musical instrument vibrates it does not make a simple oscillation with both ends fixed and the center making maximum movement. Actually the string can also vibrate in many different modes. It can vibrate as if it consists of 2, 3, 4 or higher integral number of segments with the points at midway, one third and two-thirds or every quarter of the length not moving at all. These points are called Nodes. You can see these movements in the animation below.
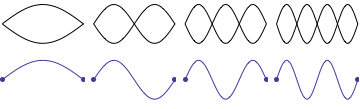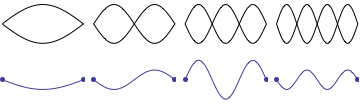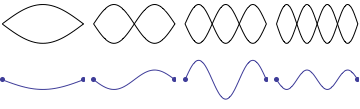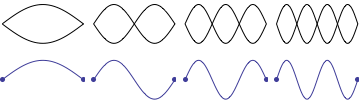
[Animation courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State]
The different modes are shown separately for clarity. In practice they occur simultaneously. The different proportions of these harmonics dictates the timbre. The frequency produced by the first (single loop) is called the 'fundamental' and the subsequent frequencies are called the 2nd,3rd,4th harmonics and so on. The second harmonic is also called 1st overtone, 3rd harmonic 2nd overtone etc.
The frequency of a vibrating string depends on the weight per unit length , how tightly it is stretched (tension) and how long the vibrating part is. Other things being equal, in the case of an 'ideal string', the frequency is inversely proportional to the vibrating length i.e. if the length is half, the frequency is double. So when a string vibrates in 2 segments it produces double the frequency, in 3 segments, three times the frequency and so on. (In Piano the frequencies of the upper harmonics are slightly higher then integral multiples and this leads to what is called 'Octave Stretch' with slightly sharpened upper notes)
The relative strengths of these different modes can also vary widely and we have hundreds of possible combinations, which explains the wide variety tones from different musical instruments. What is true of ideal strings is also true of air columns, vocal chords and almost any object producing sound. In general a flute or whistle like sound has less harmonics while stringed instruments are rich in harmonics. In the case of vibrating membranes (on drums) the harmonics may not be exact multiples of the basic frequency. In fact one of the important requirements of sustained musical note is that its harmonics should be 'true' or whole multiples of the fundamental. If you have an audio device (or software) with 'graphic equalizer' you can hear how the tone changes when the harmonics are adjusted. Speech also requires higher harmonics for clarity which is often the reason for very elderly persons' inability to follow the speech even though the sound is heard. The terms 'treble' and 'bass' imply higher and lower harmonics respectively. Absence of harmonics makes tone rather dull while very high harmonics make them sound 'metallic'.
Listen to note of a plucked string with some harmonics and listen the same note with much less harmonics -sounding 'dull'. Listen to note of frequency 524 with no harmonics and Listen to same note with high harmonics
Of the 3 attributes of sound, it is pitch that has been given maximum importance
in musical theory . A musical note can be defined as a sound where the pitch
is constant for some period (say at least one twentieth of a second - but
generally much longer). When there is a certain relationship among the pitches
of notes they sound pleasant when heard in succession (melody) or heard
together (harmony). It is found that when two notes whose frequencies are in
simple ratios are heard together or in succession they are pleasant. The
simplest ratio of 2 (one note being twice in frequency of the other) gives
maximum blending when heard together and pleasant when heard one after
the other. Listen to two notes
with frequencies in the ratio 1 : 2, first heard
in succession and then sounded together. For this reason same symbols are
used for notes whose frequencies are in the ratio 1:2, 1:4, 1:8 etc. with suitable
indications. The interval between a note and another with twice its frequency
is called an octave because in most musical systems 7 notes are used before
reaching the 8th note with double the frequency. The next best blending is
where one note is 1.5 times in frequency of the other note.
Listen to such a
pair of notes in the ratio 2: 3, in succession and together. 2:3 is the inverse of
3:2 and since a note of double frequency blends completely notes with frequencies in the
ratio 3:4 also blend as well as the notes of the ratio 2:3. Also listen to notes which are not in simple ratio - not very pleasant.
When a note of frequency (say) 400 is sung or played on a musical instrument it also has the harmonics with frequencies 800, 1200, 1600 etc. When another note with 1.5 times the frequency of 400 i.e. 600 is played we also hear the harmonics of 1200, 1800, etc. The common figure 1200 in these two notes makes them blend well. The ratio 1:2 blends thoroughly because the second note is the 2nd harmonic of the first note. When the ratio becomes smaller (say) 9:8 the blending is less as we have to hear the 10th harmonic (9 times) the first and 9th harmonic (8 times) the second (for the base of 400, the second note will be 450 and the harmonics 9 X 400 = 3600 and 8 X 450 = 3600). Generally very high harmonics are weak. But we can find another note i.e. with frequency 600 (1.5 times 400) which blends with both since 600 = 400 X 1.5 and 600 = 450 X 4/3. Listen to the notes in the frequencies 400, 600, 450 and 600 again.
The ratio 1.5 or 3:2 plays an important part in musical theory. In Indian Music it is called Samvaadhithva and ancient Sanskrit and Tamil texts describe generation of scales using this ratio. This process is called the 'cycle of fifths'. If we take any note as sa then the note which is 1.5 times in frequency is pa (in western notation C and G). Pa is the 5th note in sa-ri-ga-ma-pa and hence the term cycle of fifths. We can calculate the frequencies of a number of musical notes by repeated multipli cation by 1.5 and dividing by 2 whenever the frequency goes above twice the frequency of sa so that we get a note within the octave.
In melodic music the actual frequency is less important than the ratio between the frequencies. In Carnatic Music the musician is at liberty to chose any frequency as his tonic and then it becomes sa. In discussing frequencies of notes we use 'Relative Frequency' (r.f.) which is a ratio rather than the actual frequencies. Thus pa has the r.f. of 3/2 or 1.5 which means that the actual frequency of pa will be 1.5 times the frequency of Sa. By applying cycle of fifths 5 times we can get the following frequencies: 1 (the tonic), 3/2 (pa), 9/8 which is 3/2 X 3/2 = 9/4 divided by 2, 27/16 (9/8 X 3/2) and 81/64 (27/16 X 3/2 /2). These are roughly the white notes sa, pa, ri2, da2 and ga2. Arranging in ascending order sa,ri2,ga2,pa,da2 and adding upper Sa the r.f's are 1, 9/8, 81/64, 3/2, 27/16 and 2. Listen to these notes (you can perhaps recognize Mohanam). Continuing, we get 243/128 (ni2) and taking 4/3 as ma1 we get all the white notes (not exactly, as on the keyboard which uses equally tempered scale - explained later). To avoid more unwieldy figures we can use 15/8 instead of 243/128; these are very close (differ only by 81/80) and go further to get more notes (notes of black keys ma2,ri1,etc.)
We can also calculate frequencies by multiplying by 4/3 instead of 1.5 (cycle of fourths as 4/3 represents the fourth note from sa). Trying the cycle of fourths we get the ratios 1, 4/3 (ma1), 16/9 (4/3 X 4/3 ni1), 32/27 (16/9 X 4/3 /2 ga1) and 128/81 (32/27 X 4/3 da1) or 1, 32/27, 4/3, 128/81, 16/9 and 2 in ascending order. Listen to these notes. (Can you recognize Hindholam ?).
The diagrams below will help identify the notes in the cycle of fifths and fourths. On a keyboard or fretted instrument there are 12 notes in the octave and pa is at the 7th position and ma1 is at the 5th position. So, to apply the cycle of fifths we count 7 notes up each time (counting all the notes - black and white keys) and if the result is above the upper Sa we come back by 12 notes to be within the octave. On a cyclic diagram this is automatically done. For cycle of fourths count 5 notes each time. (Colors of the lettering correspond to key colors.)
There is a catch in calculating frequencies by cycles using 3/2 and 4/3 as ratios
because 3/2 multiplied 12 times is 129.746.. and dividing by 2 repeatedly to
come back to the octave we land up at 2.027.. instead of 2 which should be the
r.f. of upper Sa. In fact the pa arrived at by cycle of fourths is 1.4798 and not 1.5.
Listen to natural sa- pa and the cycle of fourth sa-pa and the two pa's
one after the other. Calculation of the frequencies by cycle of fifths and fourths
gives two sets of values for the notes differing by the fraction 81/80 which has
dogged musicians especially for orchestration involving extensive harmony.
From these pairs of notes the following set of simple fractions are generally
mentioned for 'natural notes':
| sa | (ri1) | ri2 | (ga1) | ga2 | ma1 | (ma2) | pa | (da1) | da2 | (ni1) | ni2 | Sa |
| 1 | 16/15 | 9/8 | 6/5 | 5/4 | 4/3 | 45/32 | 3/2 | 8/5 | 5/3 | 16/9 | 15/8 | 2 |
Although 9/8 (ri2) and 3/2 (pa) have a relative ratio of 4/3, the ratio between da2 (5/3) and ri2 (9/8) is 40/27 and not 3/2. There is no way to have every pair of notes separated by 7 or 5 notes to have the perfect 3/2 or 4/3 ratio. As this problem caused difficulties in orchestration, western system has adopted a scheme in which every adjacent pair of notes has the same r.f. of twelfth root of 2 - about 1.05946. This is called the 'equally tempered scale'. In this scheme ma and pa are 1.3348 and 1.4983 instead of 1.3333 and 1.5, a difference not usually distinguishable by the human ear (0.1 percent).
The idea of simple ratio for notes can be illustrated on stringed instruments.
Most stringed instruments have a few strings only and notes are produced by
damping a part of the string (on the finger board on a violin or on the frets
in Veena or Guitar) and making the rest vibrate. By damping lengths which are
simple fractions like 1/2, 1/3, 1/4 etc. we can get pleasant notes of r.f. 2,3/2,4/3
etc. The relative frequency is the reciprocal of the vibrating part fraction. The
ratios 2 (Sa of upper octave), 3/2 (pa), 4/3 (ma1), 5/4 (ga2) and 6/5 (ga1) are all
natural notes because of their simple ratios. 7/6 and 8/7 are however not used
but 9/8 (ri2) and sometimes (10/9) are used. The sketch below shows how notes
are generated by damping part of a 60 cm long string. In a fretted instrument there is
some pressure applied to make string contact the fret and this increases the tension and
actual positions would be slightly to the left.
The process of cycle of fifths or fourths is actually visible on stringed instruments
especially those with frets. Different notes are produced on the different strings
at a given fret. The Veena has its first string tuned to sa and the next to lower
pA with r.f. 3/4 (3/2 / 2). Thus on every fret, the frequency of a note on the
pA string is 3/4th of the note on sa string because the vibrating lengths are
reduced by the same proportion in both cases. Against the pa fret of sa string
we get ri2 on the pA string, against ri2 on sa string we get dA2 on pA string,
against da2 of sa string we get ga2 on the pA string and so on, generating the
same sequence of notes as in the cycle of fifths. In fact this is how the frets are
placed. If pa fret is placed correctly others can be placed by alternately
listening to notes produced on sa and pA strings. If we tune the second string to
mA we will get the notes of the cycle of fourths.
As mentioned earlier the slight increase in tension when the string is pressed to the fret
requires some adjustment. In the Guitar it is done by a slanting saddle next to be bridge.
The question as to the frequencies of notes used in Carnatic Music has been
subject of much discussion. The pairs of frequencies obtained by cycle of fifths
and cycle of fourths have been equated with the 22 sruthis of ancient texts - without
theoretical justification or based on practical measurements with modern computers . It
is difficult to speak of frequency when a note is constantly oscillated, often with
unequal timings of rest at the ends. When ri1 of Saaveri is sung the voice
remains most of the time in sa and reaches ri1 quickly and comes back giving
the feeling of a very low ri1. It is possible that the presence or absence of other
notes with sa-pa or sa-ma relationship in a raagam influences the pitch of
a note and the manner in which it is held. However, some notes on the key-
board (equally tempered scale) such as ga2 (r.f. 1.26) appear somewhat higher
for an ear accustomed to the natural ga2 (r.f. 1.25 a difference of about 1% )
Listen to sa-ga equally tempered, sa-ga natural and the two ga's.
The difference is noticeable when sounded one after other and in other cases a background
properly tuned thambura sound may also help to distinguish the two notes
Given below are the frequencies of equally tempered scale and one possible
set of natural notes for sa at 262 (261.62 to be accurate, which corresponds to
440 for for da2, standard used in western music). Notes of black keys are in brackets.
Actually the notes of black keys sound much lower in Carnatic Music as they are usually
oscillated from the lower note (except ma2 which is oscillated from pa and
sounds higher).
In Music Pitch frequencies are related by ratios. Thus a note which is one octave higher has double the frequency of the lower note. A note having 3/2 times the frequency of another note is called the fifth (pa in Carnatic Music). Comparison of pitch values of fractions like 9/5 or 16/9 is difficult. The cyclic cent system coverts the ratios into additions by use of logarithms. As most music systems use 12 notes in an octave, the value of 1200 cents is assigned to a note having double the frequency of the tonic (sa and Tara Sa in Carnatic Music). In equally tempered scale each note will be (dividing 1200 by 12) 100 cents higher than the adjacent lower note . The cyclic cent of a ratio (relative frequency or rf) is given by log(rf)*1200/log(2). You will find that it is easier to appreciate the difference between 9/5 (1017.6) and 16/9 (996.1) and see which is higher. Some common note values are 'pa' (3/2)-702 cents. 'Suddha ma' (4/3) 498 cents. Adding them you get 1200 which is the value of Tara Sa. Others - Anthara Gaandhaaram 5/4 is 386, Chathusruthi Rishabham (9/8) is 204. Add 702(rf of pa) to 702 giving 1404. Subtract 1200 to come within middle octave giving 204 an this is Chathusruthi Rishabham - first step in Cycle of Fifths
In most papers or articles discussing frequencies/pitches in music the cent system is used rather than the r.f. itself. Below you can enter r.f. and get cyclic cents
Enter Relative Frequency-as decimal fraction (like 1.25)
Cyclic Cents
The pages above were meant for students whose main subject is music, as supplementary knowledge and so covered the basics without mathematical formulae or extensive video/audio.
1. Topics not covered in the pages above but may be relevant (I will try to add these with graphics and audio):
1.1 Beats: When 2 sounds differing in frequencies by a small number 'n' are sounded together, a single frequency (in between the two) varying in intensity 'n' times a second is heard. These are called beats and may be used in tuning. Persons familiar with trigonometry may see the play of 'product formula' here.
1.2 Formants: Independent of the actual frequency of the fundamental, certain range of frequencies in the higher harmonics are amplified. These are called formants and are very important in speech recognition, vowels and consonants having specific ranges. Thus if some one says "aa" or "ee" in the same pitch the difference will be in the harmonics dictated by the shape of the mouth and vocal tract. They also give you the feel of the instrument independent of the pitch.
1.3 Envelopes: One characteristic of instruments especially plucked strings is the envelope -the manner in which the intensity increases and then declines. This is usually defined by four phases - attack (quick increase), decay (a quick fall) ,sustain (long steady),release(falling to zero).
1.4 Wind instruments: Modes of vibration - closed at one end open at both ends.
1.5 Percussion instruments:: how Mridangam and Tabala overcame the inharmonicity of vibration of membranes.
1.6 Speciality of Indian stringed instruments like Veena, Sitar, Tambura etc.
2. 22 Sruthis- I have not touched this topic. Much has been written and frequencies assigned without any support from old texts. Modern researchers using computers for analysis have found that the 22 sruthis concept has no relevance for todays melodic music. I will include this in an article meant to dispel common misconceptions of music researchers when they enter the realm of Physics.
3.If you are interested more on the subject of physics of sound with mathematical formulae you can read this book (about 100 pages) available on line:
THE PHYSICS OF MUSIC AND MUSICAL INSTRUMENTS
This printed and much larger book may be in your library: "The Science of Sound" by T.D.Rossing (Addison Wesley)
(This book covers the topic of 'inharmonic' tones of piano strings - p 175 of 1981 edition)
4. If you are interested in analyzing live music the free software 'Praat' is available. For Windows PC it requires no installation. (It is available for Mac and Linux also.) It was originally written for speech/phonetics analysis and may be used for music analysis also. Download the zip file, open it, extract the single .exe file and run it. The program requires lot of trial to use it for your specific requirement as it has variety of interfaces.
Link for the Windows version
There is a tutorial file in .pdf format and another for musicologists. You may get them by searching. The Help part of the Praat program itself is not very useful for beginners.
Copyright:2021 M.Subramanian, India. All rights reserved (all pages, links and code)
or in a/b style (like 5/4) and click OK
r.f.
https://murobox.com/wp-content/uploads/2023/07/Lapp.pdf
https://www.fon.hum.uva.nl/praat/download_win.html